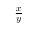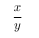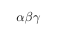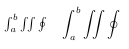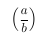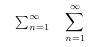What is math mode?

For many people the most useful part of LaTeX is the ability to typeset complex mathematical formulas. for the sake of simplicity, LaTeX separates the tasks of typesetting mathematics and typesetting normal text. This is achieved by the use of two operating modes, paragraph and math mode. There is also a third mode called LR mode, however, this is rarely used by beginners and furthermore, is usually implicitly entered with other commands. It will not be covered here. Paragraph mode is the default mode for the document environment and does not need to be called explicitly.

There are a few ways to enter math mode, however the most common is $....$, where the text within the dollar signs is in the math mode environment. You have already been using math mode unknowingly by using the \begin{equation} and \end{equation} commands.

The following table lists three methods and their usage of declaring math mode.

There are equivalent ways of entering math mode for each of these methods, for example, $$....$$ is equivalent to \[ ....\], however, the latter is now strongly preferred. I almost always use the first two methods for typesetting basic math.

Now try the following LaTeX code.

\documentclass{article}
\begin{document}
\begin{equation}
	\int_\alpha^\beta f'(x) \, dx=f(\beta)-f(\alpha).
\end{equation}
We can use the fundamental theorem of calculus to say that
 $\int_2^3 x^2 \, dx=\frac{3^3}{3}-\frac{2^3}{3}=\frac{19}{3}$.  
Also note that $\displaystyle \int_2^3 x^2 \, dx=\frac{3^3}{3}-\frac{2^3}{3}=\frac{19}{3}$. 
 We can also give this equation its own line 
\[
	\int_2^3 x^2 \, dx=\frac{3^3}{3}-\frac{2^3}{3}=\frac{19}{3}.
\]
\end{document}

Note that math mode ignores whitespace, in fact, this whole code could have been put on one line and still would have compiled correctly. Another thing to notice is the effect of the \displaystyle command. This command forces LaTeX to give an equation the full height it needs to display as if it were on its own line. Be careful in using it as it can make a document due to variable line height.

Multiple Equations

There are several ways to format multiple equations and the amsmath package adds several more. In general, the command \\ signifies a line break and within the correct math mode environment, it can start a new equation line. Try the example on the right which sets the same multiple equations in several ways.

Observe that the equation environment does not even allow line breaks. this is not the proper environment for multiple equations if we wish to have them formatted on separate lines.

The gather and align environments both give us the result we want, albeit in slightly different manners.

• If we use the gather environment, every equation is centered.
• If we use the align environment and insert an & on every line where we wish the equations to be aligned (usually at some sort of equality symbol), the equations will be aligned.

The following is a table of some of the most common LaTeX mathematical symbols.

Symbol Name	LaTeX Command	Rendering	Notes
Fraction	\frac{x}{y}
In-line Fraction	\dfrac{x}{y}		Similar to \displaystyle with \frac
Greek Letters	\alpha \beta \gamma
Integral	\int_a^b \iint \oint		Second set have \displaystyle
Properly sized parentheses	\left(\dfrac{a}{b}\right)		Will automatically size
Summations	\sum_{n=1}^\infty		Second set have \displaystyle